-
Matemātika
Evaluated!
Atrisināšanas paņēmieni:
1. Ievietošanas.
Risina izsakot vienu no nezināmajiem un pēc tam šo izteikto nezināmo ievieto otrajā vienādojumā un tālāk risina kā parastu vienādojumu.
2. Saskaitīšanas vai atņemšanas.
Vienādojuma sistēmas abus vienādojumus atņem vai saskaita tā, lai paliek tikai viens nezināmais, un tālāk risina kā parastu vienādojumu.
3. Grafiskais.
Izsakot abu sistēmas vienādojumos abus y un pēc šī vienādojuma veido divus grafikus, tad to krustpunktā arī ir vienādojuma saknes.
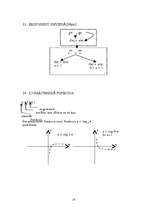
Vai nevienādību x2>25 apmierina x>5? Vai var teikt, ka ar atbildi x>5 nevienādība x2>25 ir atrisināta?
Par kvadrātnevienādībām ar vienu nezināmo sauc nevienādības, kas pārveidojamas vai jau dotas formā ax2+bx+c>0 (arī ar nevienādības zīmēm <, ≤, ≥). Te x ir nezināmais, bet parametri a, b un c ir jebkuri doti skaitļi ar a≠O.
Nevienādības ax2 + bx+c>0 kreisajā pusē ir argumenta x kvadrātfunkcija y=ax2+bx+c. Tādējādi prasību atrisināt doto nevienādību var uztvert kā funkcijas y=ax2+bx+c pētīšanu, nosakot, ar kādām argumenta x vērtībām šī funkcija ir pozitīva (negatīva, nenegatīva, nepozitīva). Šajā nolūkā pietiek uzskicēt šīs funkcijas grafiku, kurā precīzi fiksēti tikai parabolas krustpunkti ar x asi, t. i., punkti, kuros funkcijas vērtība ir nulle. Pēc tam nevienādības atrisinājumu ir viegli nolasīt no grafika.
L piemērs. Atrisināt nevienādību x2-x> 6.
Aizstājam doto nevienādību ar tai ekvivalentu nevienādību normālformā: x2-x-6>0.
Atrodam funkcijas y=x2-x-6 saknes: xļ = -2, x2=3 (pēc Vjeta teorēmas).
Uzskicējam visai aptuvenu funkcijas grafiku (74. zīm.), ievērojot tā krustpunktus ar abscisu asi un parabolas zaru virzienu (šajā piemērā - zari uz augšu, jo kvadrātlocekļa koeficients a=l>0).
Piezīme. Pietiek norādīt tikai koordinātu plaknes abscisu asi, nenorādot pat koordinātu sākumpunktu un vienības nogriežņa garumu.
Iekrāsojam un nolasām intervālus, kuros funkcija y = = x2—x—6 ir pozitīva jeb kas reizē ir arī dotās nevienādības x2-x>6 atrisinājumi.
Atbilde: x<-2 vai x>3 jeb x€(-∞; -2)U(3; +∞);
2. piemērs. Atrast nevienādības x2-x-6≤0 atrisinājumu kopu.
Risinot līdzīgi kā nevienādību iepriekšējā piemērā, no jau pazīstamās funkcijas y=x2-x-6 grafika nolasām atbildi: -2
Aizstājam šo nevienādību ar tai ekvivalentu nevienādību normālformā -2x2+16x-32 >0. Dalot tās abas puses ar -2, iegūstam vēl vienkāršāku nevienādību x2-8x4-16<0.
Atrodam funkcijas y=x2-8x-16 saknes: x=4; x2 = 4.
Uzskicējam funkcijas grafiku (75. zīm.).
Grafiks uzskatāmi parāda, ka nav tādu argumenta x vērtību, ar kurām funkcija y=x2- 8x+16 būtu negatīva. Tātad ari dotajai nevienādībai - 2x2 > 32 –16x nav atrisinājuma. Atbildi var norādīt arī ar tukšas kopas simbolu: 0.
4. piemērs. Atrisināt nevienādību x2-8x+ 16 >0.
Risinot līdzīgi kā iepriekšējā piemērā, no grafika (75. zīm.) nolasām un pierakstām nevienādības atrisinājumu: x<4 vai x>4. Vai xe (-∞; 4) (J (4; - ∞). Arī: x - jebkurš skaitlis, bet x≠4.
5. piemērs. Atrisināt nevienādību –2x2 + 3x-5≤0. Aizstājam doto nevienādību ar «patīkamāku» ekvivalentu nevienādību 2x2-3x 4-5>0.…
Pilniigi viss ko var iedomaaties matemaatikaa: 1.SKAITĻU KOPAS 1. Naturālo skaitļu kopa N Par naturāliem skaitļiem sauc skaitļus, kas rodas skaitīšanas procesā. Šie skaitļi veido naturālo skaitļu kopu, kuru var pierakstīt kā bezgalīgu skaitļu virkni:...